The Logical Hexagon Made Simple

by: Greg Boyd

The Hexagaon in a Nutshell

For those of you who don’t have the twenty to thirty minutes it will probably take to read this essay but who nevertheless would like to have some idea of what the Logical Hexagon is all about, here is my two sentence elevator speech:

The Logical Hexagon demonstrates that, on the assumption that people possess free will, then the future must be described not only in terms of what WILL and WILL NOT come to pass, but also in terms of what MIGHT and MIGHT NOT come to pass. And precisely because an omniscient God must know the whole of reality exactly as it is, God must know the future partly in terms of what MIGHT and MIGHT NOT come to pass. 

A Slighter Longer Explanation

And now, for those who have the time, here is a fuller explanation.^[1]

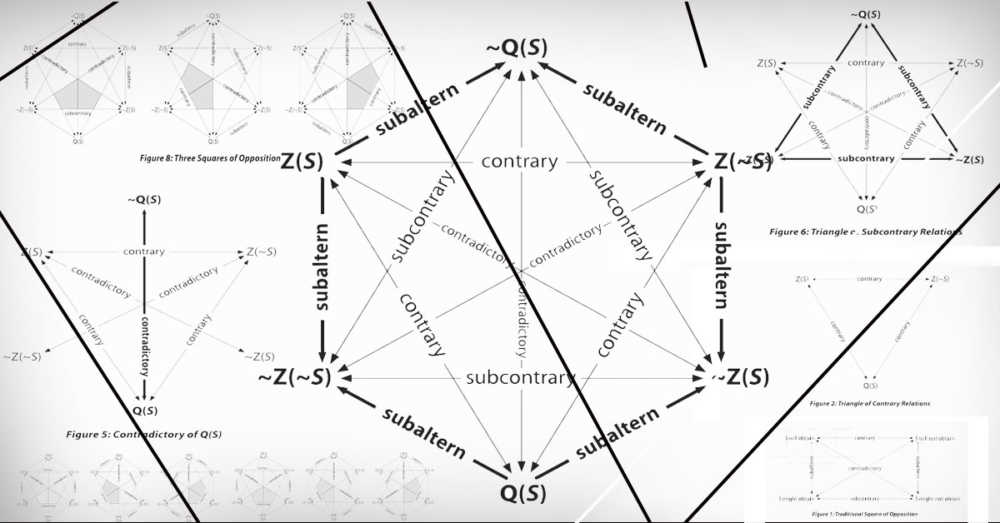
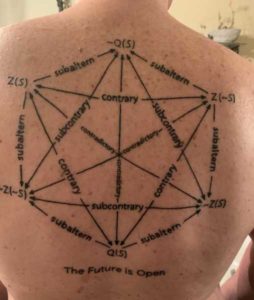That tattoo on my back is formally called the “Hexagon of Opposition” because it claims to correct and improve upon Aristotle’s famous “Square of Opposition.” But “opposition” sounds rather combative to non-logicians, so I prefer to refer to this diagram simply as “the Logical Hexagon,” or simply as “the Hexagon.” This Hexagon was created by Alan Rhoda, Tom Belt and myself in 2005 in response to a defect we discerned in Aristotle’s Square that prejudiced western logic in a deterministic direction. In the process, we discovered that the Logical Hexagon also makes clear why acknowledging that God doesn’t know what a future free agent will choose to do does not in any way qualify God’s omniscience. And the Hexagon has a number of other potential philosophical and/or theological implications as well, as I’ve argued in several articles.^[2]

Almost from the start I felt that the Hexagon was simply too elegant not to be true, so much so that I promised myself that I would have it tattooed on my back if I ever became sufficiently convinced it was valid. Well, thanks to the brilliant defense of the Hexagon by Elijah Hess against the critiques of William Lane Craig and others, I’ve decided I’m probably as convinced as I’m ever going to be.^[3] So, on Tuesday, January 7th, 2020, my friend and Tattoo-artist extraordinaire, Cliff Clayton, graciously volunteered to tattoo the Hexagon on my back in exchange for nothing more than some  one-on-one theology talk time. It obviously was a very gracious offer on Cliff’s part!^[4]

In a previous post I  talked about the (shockingly unpleasant!) experience of getting this tattoo (link).  Today I’d like to explain the Hexagon itself in as short and simple terms as possible.

 I’ll admit up front that communicating the Hexagon simply isn’t easy, for the Hexagon employs philosophical terms, symbols, and formulae that most people are unfamiliar with.  I did my best, but be forewarned: you may come upon sections in this essay that strike you as rather dense. I encourage you to plough through them. I think you’ll find that, more often than not,  the challenging material is explained by subsequent easier material.

The payoff for your effort is not simply that you’ll understand an awesome looking logical diagram. If you press through this, you may just find yourself beginning to think about God, the future, free will, and providence in a more beautiful and a more helpful way.

I’ll start by introducing the several key logical terms as well as the three symbols (called “logical operators”) found on the Hexagon. I put this material upfront as a sort of prelude since I suspect some readers may find it helpful to come back to this section to refresh their memory as they read this essay. Following this, I will provide a brief explanation and critique of  Aristotle’s Square of Opposition, arguing that it is prejudiced toward determinism. And I will then lead readers through the three steps that transform Aristotle’s Square into the Logical Hexagon.  

———-

Key Terms

Contradictory: A proposition holds a contradictory relationship with another proposition if and only if one of the two propositions must be true and the other false. 

Contrary: A proposition holds a contrary relationship with another proposition if and only if they cannot be conjointly true but may be conjointly false. 

Subcontrary: A propositions holds a subcontrary relationship with another proposition if and only if the propositions cannot be conjointly false but may be conjointly true. Subaltern:  A proposition holds a subaltern relationship with another proposition if and only if the truth of one proposition entails the truth of another, while the converse is not true. 

Logical Operators

Z =  “settled”; “will definitely happen,”  “definite fact”

Q = ““unsettled”, “might and might not happen,” :indefinite possibilities”

S = “future state of affairs”  

~ = not

Hence,

Z(S) = S will come to pass 

Z(~S) = S will not come to pass 

Q(S) = S might and might not come to pass

Aristotle’s Square of Opposition 

There are three distinct ways that we may speak about future events .  We may say that a particular future event (S) “will obtain” (=”come to pass”). We may say that this event (S) “will not obtain.” Or we can say that this event (S) “might or might not obtain.”  To illustrate, it  may be true that Sam will buy a blue Toyota at 3:10PM on June 12th, 2025 (henceforth BT25). Conversely, it may be true that Sam will not buy a BT25. Or, it may be true that Sam might and might not buy a BT25. 

On Aristotle’s traditional Square of Opposition, the logical relationships between these three ways of describing the future are as follows.

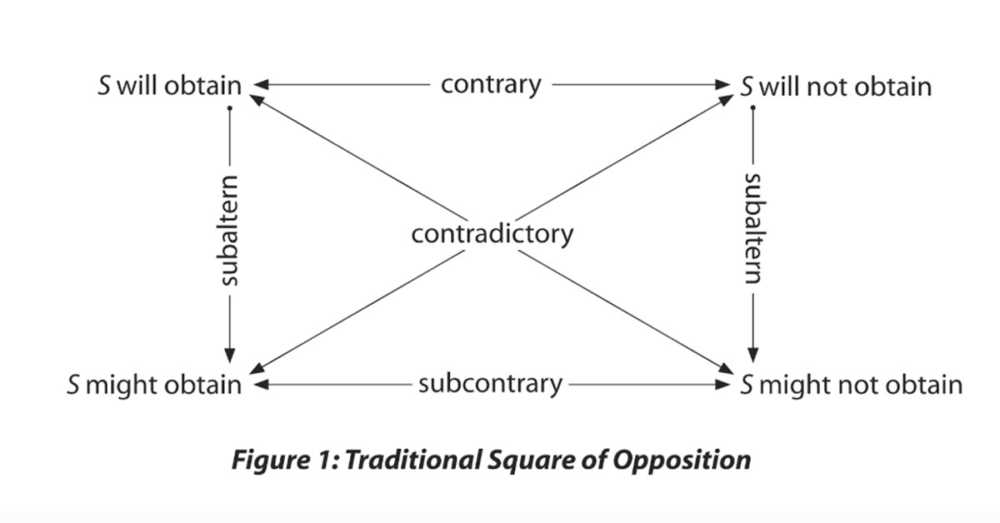
Rhoda, Belt and I noticed a curious defect in Aristotle’s Square. It is prejudiced toward determinism in as much as it has a distinct logical operator to assert “S will obtain” [Z(S)] and to assert “S will not obtain” [Z(~S)], but to affirm “S may or may not obtain,” one must affirm the conjoint truth of the two subcontrary relations (“S might” and “S might not” obtain).  The Logical Hexagon began with the realization that a comprehensive logical map of the logical relationships that pertain between propositions asserting one of the three logically possible future state of affairs ought to express the open dimension of the future (“might and might not’) as fundamentally as it expresses the settled dimension of the future (“will” and “will not”). The open dimension thus ought to be represented by its own logical operator (Q).

I will now review the three steps that were taken to transform Aristotle’s Square into the Logical Hexagon.

1. The Triangle of Contrary Relations

To begin, lets inquire into the logical relationship that exists between propositions asserting these three possible future state of affairs,  Z(S), Z (~S)), Q(S). When any one of these three obtains, the other two cannot. Since no two of these three possible future states can be conjointly true, while two of the three must be conjointly false, propositions asserting these three possible future states of affairs are related to each other as contraries, which can be illustrated as follows:

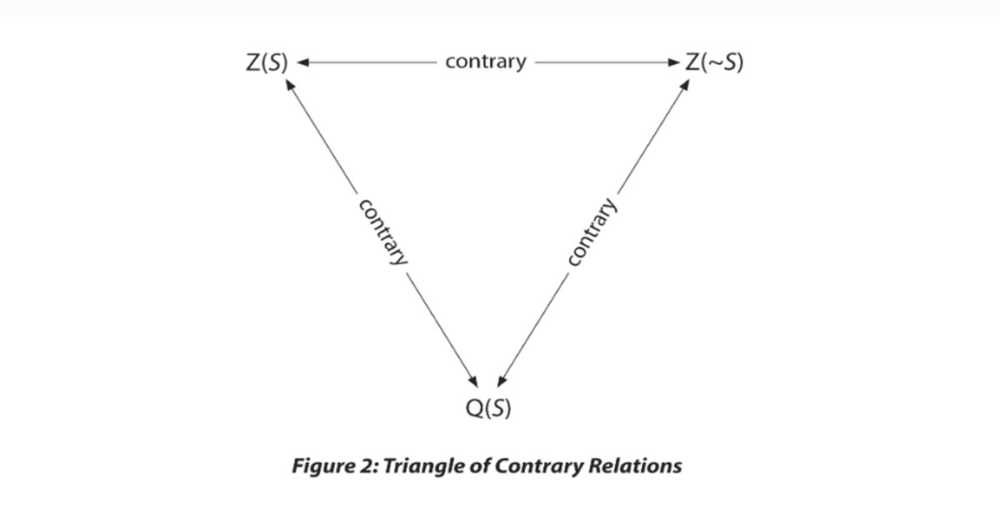
Notice that, if it is true that the future is as yet unsettled as to whether or not Sam will buy a BT25 [Q(S)] , then it is false both that Sam will buy a BT25 [Z(S)]] and false that Sam will not buy BT25 [Z(~S)].  I grant that sounds counterintuitive, since Sam obviously either will or will not end up buying a BT25.  However, while it’s true that Sam will eventually choose to buy a BT25 or not, this doesn’t mean that the truth of what he will end up choosing predated his choosing it. 

Philosophers frequently note that common language is designed for common use, which is why it is often inadequate at capturing philosophical nuances. This is certainly the case when it comes to talking about the three possible future states of affairs. To clarify how Z(S) (“will”) and Z(~S) (“will not”) can be conjointly false, we simply need to note that Z(S )and Z(~S) assert a definiteness over the future that Q(S) denies. .  To assert that “Sam will or will not buy a BT25” is to assert that “Sam will definitely,” or  “Sam will definitely not buy a BT25.” In other words, to say “will” or “will not” is to assert a settled fact about the future that negates the possibility that things might turn out otherwise. 

By contrast, to assert that “Sam might and might  buy a BT25” is to deny that there is any definite fact of the matter about whether Sam  will or will not purchase a BT25. Hence, if it is true that Sam might and might not buy this car on this date, then it is false both that Sam definitely will buy this car on this date — because he might not — and false that Sam definitely will not buy this car on this date — because he might. Hence, if Q(S) is true, the contrary relationships Z(S) and Z(-S) must both be false.  

There are three significant implications that follow from this Triangle of Contrary Relations.  First, it demonstrates that it is logically possible for the future to be genuinely open, to one degree or another. And, while I can’t make the case now, I would argue that this logical possibility must be accepted as a description of the actual future if you accept, , as I do, that the Creator has endowed humans (and possibly other agents) with morally responsible free will.  This will empower us to resolve a multitude of possible courses of action into one actual course of action. 

Hence, prior to my resolving a number of possible decisions into one actual decision, the only fact-of-the matter pertaining to my future decision is that I might choose X or that I might choose Y. Hence, prior to my decision, it is false both that I will (definitely) chose X and false that I will (definitely) not chose Y. Moreover,  since an omniscient God must know reality exactly as it is, God would not know what I will (definitely) or will (definitely) not do, precisely because God perfectly knows what I might and might not do.^[5]  As the Bible itself indicates, this entails that, insofar as people  possess free will, God must think about the future in terms of what might or might not happen rather than exclusively in terms of what will and will not happen.^[6]

Second, against the dominant strand of the western philosophical tradition, this Triangle of Contrary Relations makes it clear that the truth value of propositions asserting future states of affairs that might or might not come to pass (Q) are not timeless.  While it may be true prior to 2025 that “Sam might or might not buy a BT25,” as the date of this possible purchase approaches, it will inevitably become true either that ‘Sam will [definitely] buy a BT25,”  or that “Sam will [definitely] not buy a BT25.” When this happens, it will of course become false that “Sam may or may not buy a BT25.” Once a possibility becomes a settled fact, there are no “maybes” about it.  

In other words, the Logical Hexagon makes it clear that the truth value of propositions asserting future states of affairs must always be indexed to particular points in time. Whether it is true that Sam will (definitely)  or will (definitely) not buy a BT25, or whether it is true that Sam might or might not buy a BT25, depends entirely on when the statement is made. 

And third, in contrast to Aristotle’s Square, the Logical Hexagon makes clear a distinction between “might” when it is functioning as the subaltern of  “will,” on the one hand, and “might” when it is functioning as the contradictory of “will” and “will not” and when conjointly true with “might not.”   When “might” functions as the subaltern of “will,” it only expresses an epistemic limitation. If it is true that “Sam will purchase a BT25,” then we would only say “Sam might purchase a BT25” if we were ignorant of that truth. By contrast,  when “might” and “might not” are conjointly true and “will” and “will not” are conjointly false, “might” is no longer merely expressing epistemic ignorance: it is expressing an ontological state of affairs on a par with “will” and “will not” propositions, which is precisely why it warrants its own logical operator (Q). 

2. The Triangle of Subcontrary Relations

Bivalence is a rule of logic that asserts that every meaningful proposition is either true or false, which is to say, either this proposition or its contradictory must be true.  To further flesh out the logical relations that pertain between the three possible future states of affairs, I’d like to apply the law of bivalence to the three foundational poles that comprise the Triangle of Contrary Relations. When we do this, we will find that it generates a further Triangle of Subcontrary Relations. 

Consider Z(S). As we saw above, common parlance sometimes leads people to mistakenly assume that the contradictory of “Sam will buy a BT25,” is “Sam will not buy a BT25.” Yet, as I demonstrated above,  these cannot be contradictory since they can be conjointly false, as is the case when “Sam might and might not buy a BT25.” The contradictory of “Sam will (definitely) buy a BT25” [Z(S)] is not  “Sam will (definitely) not by a BT25,” [Z(~S)] but rather, “It is not the case that Sam will (definitely) buy a BT25 [~ Z(S)], which is equivalent to “Sam might not buy a BT25,”

Similarly, the contradictory of “Sam will not buy a BT25”  [Z(~S)] is not,  “Sam will buy a BT25” [Z(S)], but rather,  “It is not the case that Sam will (definitely) not buy a BT25” [~Z(~S)], which is equivalent to “Sam might buy a BT25.”   We can illustrate this as follows:

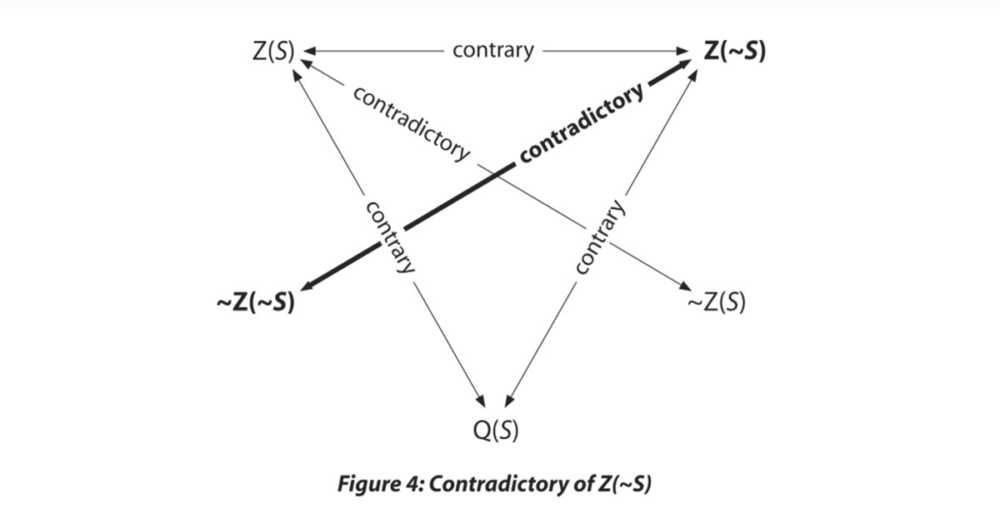
Lastly, the contradictory of the third possible future state of affairs – what “might and might not” obtain [Q(S)}–  is ~Q(S), which asserts, “It is not the case that future event (S) is unsettled, indeterminate, or open,” which is to say that it is the case that future event (S) is settled,” whether as “will” [Z(S)] or “will not”[ Z(~S)]. We can illustrate this as followers: 

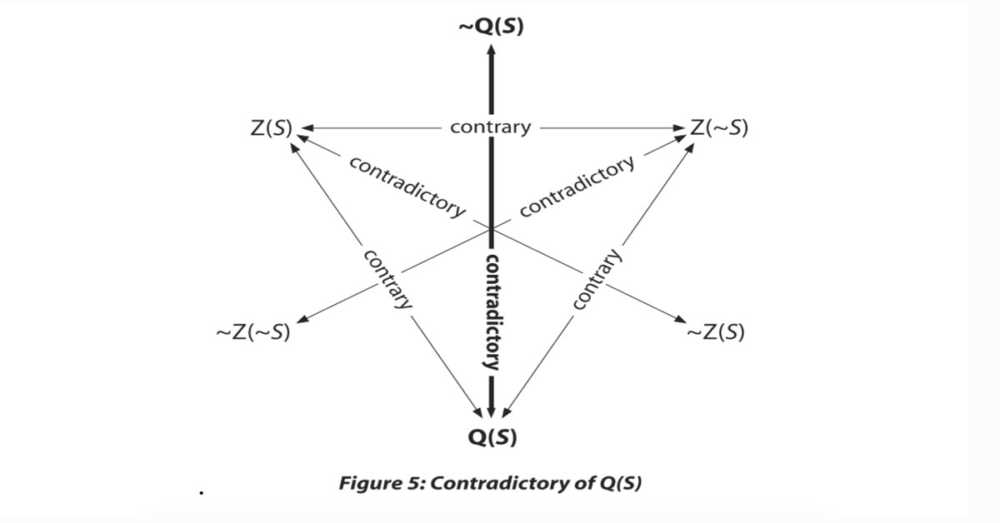
Let’s now inquire into the logical relationship between these three contradictories, ~Z(S), ~Z(~S) and ~Q(S). Fleshing out these relationships involves talking about the truth and falsehood of negations, which can get a little convoluted. Some readers might want to simply take my word for it and skip to the last sentence of the following paragraph. 

To begin, we’ve seen that Q(S) entails both ~Z(S) and ~Z(~S).  If at any given time it is true that Sam might and might not purchase a BT25, then it is false that Sam will (definitely) purchase a BT25 and false that Sam will (definitely) not purchase a BT25. But it is equally clear that ~Z(S) and ~Z(~S) cannot be conjointly false, for if ~Z(S) is false, then Z(S) is necessarily true, and if ~Z(~S) is false, then Z(~S) is necessarily true.  But Z(S) and Z(~S) cannot be conjointly true, from which it follows that  ~Z(S) and ~Z(~S) cannot be conjointly false. The same holds true for the other pairs, ~Z(S) and ~Q(S) as well as  ~Z(~S) and ~Q(S)].  For each pair, it is logical possible for both to be true but not logically possible for both to be false, which means that they are related to each other as subcontraries. These can be illustrated as follows:

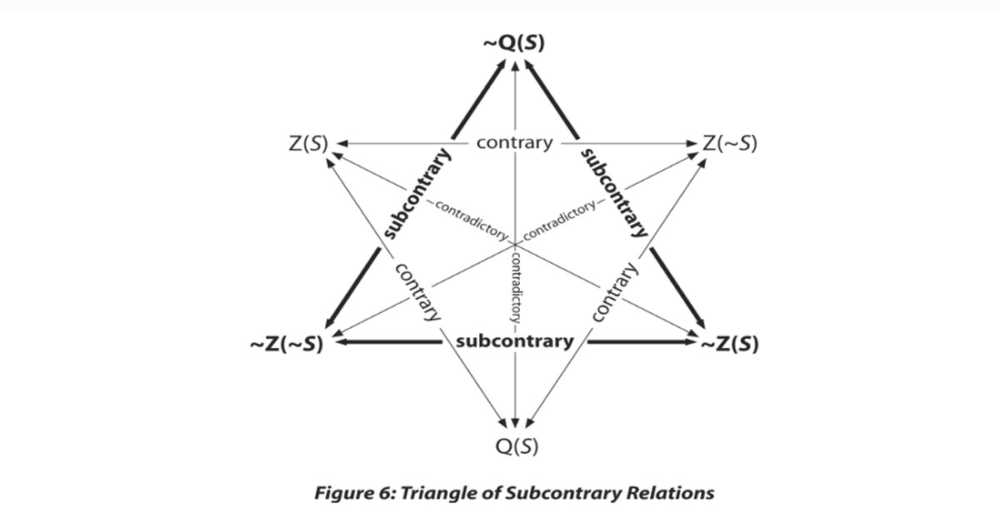
3. The Hexagon of Subaltern Relations

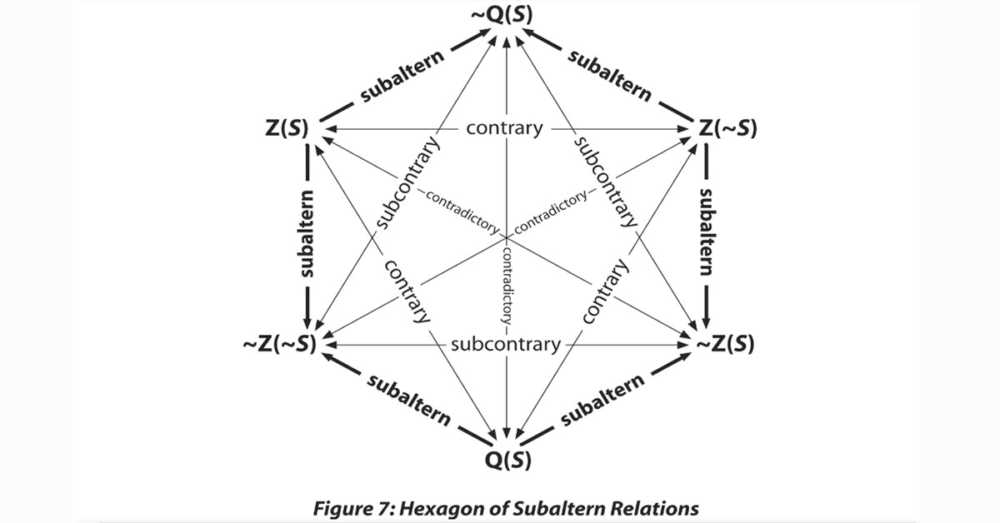
Having reviewed the contradictory, contrary, and subcontrary relations involved in the Hexagon, the final step is to explore the logical relationship that exists between the Triangle of Contrary Relations and the Triangle of Sub-Contrary Relations. This involves demonstrating the logical relations that exist between the six operators that comprise the parameter of the Hexagon. 

Consider the relationship between Z(S) and ~Z(~S).  If it is true that Sam will (definitely) purchase a BT25, then it must also be true that Sam might purchase a BT25. However, to say that Sam might purchase a BT25 does not entail that Sam will purchase a BT25, for as we’ve seen, might and might not may be conjointly true, in which case it is false both that Sam will (definitely) purchase a BT25 and false that Sam will (definitely) not purchase a BT25.  Hence, while Z(S) impies ~Z(~S), the converse is not true, which means that ~Z(~S) is the subaltern of Z (S). This same relationship connects all the logical operators that comprise the parameter of the Hexagon.  In the following illustration, which presents the Hexagon in its entirety, the one-sided arrows that form the Hexagon point toward the subaltern, 

Voila!

One More Curious Thing

There is one final cool feature of the Hexagon that I would think a nerd like yourself would want to know about (if you’re still reading this, you’re a nerd!). A short while after the Hexagon was completed, Tom Belt noticed that the Hexagon contained three versions of Aristotle’s Square, each expressing the contradictory, contrary, and subaltern relationships that pertain to each of the three possible future states. 

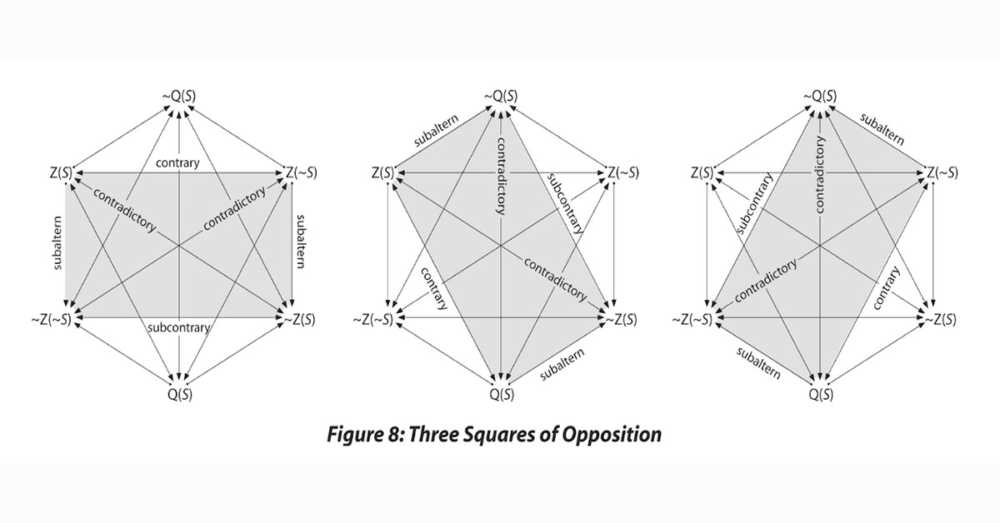
In my estimation, this triplication of Aristotle’s Square confirms that, to accurately and comprehensively map out the logical relationships that pertain to the three possible future states of affairs, we need to postulate three, not two, possible future states of being [Z(S), Z(~S), and Q(S], and the logic of Aristotle’s square needs to be worked out for each one. 

Conclusion

Most people in western culture have assumed that God knows all that will come to pass because they assumed that the future can be exhaustively defined as the realm of what will and will not come to pass.  And if this assumption is true, then denying God knows what will happen in the future is tantamount to denying omniscience. However, the Hexagon exposes the error of this assumption by making explicit something that could only be indirectly inferred from Aristotle’s Square: namely, that the future may also be comprised of what may or may not come to pass, and to this degree, an omniscient God must know the future as a domain of what may or may not come to pass.

In this light, I trust it’s clear why acknowledging that God doesn’t know what a future free agent will (definitely) choose does not imply any limitation on God’s omniscience.

Bless you,
as you move into a future
filled with possibilities!

Greg

___ ___ ___